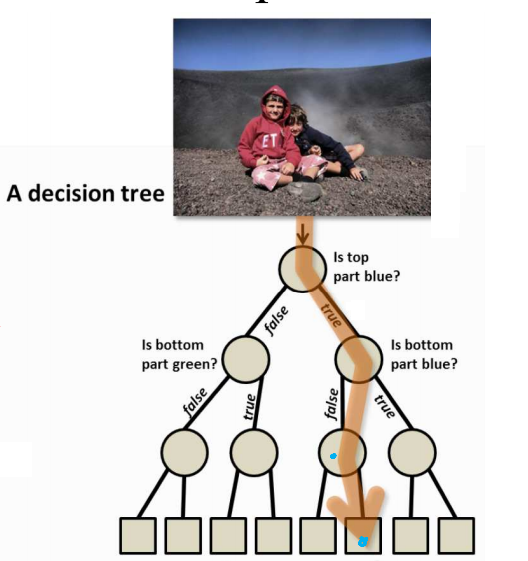
Machine learning decision tree (cây quyết định)

Cây quyết định (Decision Tree) là một cây phân cấp có cấu trúc được dùng để phân lớp các đối tượng dựa vào dãy các luật (series of rules). Khi cho dữ liệu về các đối tượng gồm các thuộc tính cùng với lớp (classes) của nó, cây quyết định sẽ sinh ra các luật để dự đoán lớp của các đối tượng chưa biết (unseen data).

I. CẤU TRÚC DECISION TREES
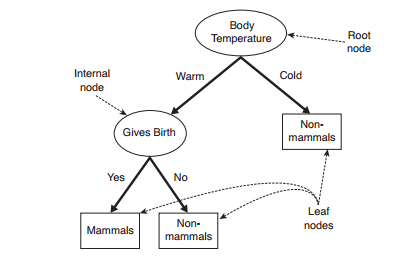
Decision Trees gồm 3 phần chính: 1 node gốc (root node), những node lá (leaf nodes) và các nhánh của nó (branches). Node gốc là điểm bắt đầu của cây quyết định và cả hai node gốc và node chứa câu hỏi hoặc tiêu chí để được trả lời. Nhánh biểu diễn các kết quả của kiểm tra trên nút. Ví dụ câu hỏi ở node đầu tiên yêu cầu câu trả lời là “yes” hoặc là “no” thì sẽ có 1 node con chịu trách nhiệm cho phản hồi là “yes”, 1 node là “no”.

II. CÁC THUẬT TOÁN LIÊN QUAN TỚI DECISION TREES

ID3 (Iterative Dichotomiser 3) Algorithm
Thuật toán ID3 có thể được tóm tắt như sau:

Lấy tất cả các thuộc tính chưa được sử dụng và đếm entropy liên quan đến mẫu thử của các thuộc tính đó
Chọn thuộc tính có entropy lớn nhất
Nối node với thuộc tính đó

ID3 (Examples, Target_Attribute, Attributes)

Begin:

Tạo node gốc
Nếu tất cả các examples (ví dụ) đều nằm cùng một lớp là dương thì return một nút lá được gán nhãn bởi lớp đó (lớp +).
Nếu tất cả các examples (ví dụ) đều nằm cùng một lớp là âm thì return một nút lá được gán nhãn bởi lớp đó (lớp -).
Nếu tập thuộc tính Attributes là rỗng thì return Cây quyết định có nút Root được gắn với nhãn lớp bằng giá trị chung nhất trong tập thuộc tính ở tập ví dụ (Examples).

Else begin:

Chọn thuộc tính A – Thuộc tính trong tập Attributes có khả năng phân loại “tốt nhất” đối với Examples
Thuộc tính kiểm tra cho nút Root ← A và lấy nó làm gốc cho cây hiện tại
Với mỗi giá trị vi của A:
- Bổ sung một nhánh cây mới nằm phía dưới node gốc, tương ứng với trường hợp A = vi
- Xác định Examples(vi) sao cho tập con của Examples có giá trị vi cho A
- Nếu Examples(vi) rỗng

# Tạo một nút lá được gắn nhãn = giá trị đích phổ biến nhất trong Examples. Sau đó gắn nút lá này vào nhánh cây mới vừa tạo.

Ngược lại, gắn vào nhánh cây mới vừa tạo một cây con sinh ra bởi ID3 (Examples(vi), Target_Attribute, Attributes – {A})

Kết thúc
Trả về giá trị node gốc

C4.5 Algorithm

C4.5 là thuật toán phân lớp dữ liệu dựa trên cây quyết định hiệu quả và phổ biến trong những ứng dụng khai phá cơ sở dữ liệu có kích thước nhỏ. C4.5 xây dựng cây quyết định từ tập training data tương tự như ID3.

Tập training data S gồm các mẫu đã được phân loại sẵn s1, s2,… Mỗi mẫu si = x1,x2,… với x1, x2 là 1 vector biểu diễn cho thuộc tính hoặc đặc điểm của mẫu. Một tập vector C = c1,c2,… với c1, c2 biểu diễn cho mỗi lớp mà mỗi mẫu thuộc về.

Với mỗi lớp của cây, C4.5 chọn một thuộc tính của dữ liệu mà phân chia tập các mẫu thành nhiều tập con, được nâng cao chất lượng một cách hiệu quả nhất. Tiêu chuẩn của nó là thu được information gain (sự khác biệt về entropy) – kết quả từ việc chọn một thuộc tính cho việc chia tách dữ liệu. Quyết định đưa ra dựa trên tập thuộc tính với information gain được chuẩn hóa cao nhất. Thuật toán C4.5 sau đó sẽ lặp lại với các danh sách con nhỏ hơn.

Một vài trường hợp cơ bản:

– Tất cả các mẫu đều thuộc cùng một lớp. Khi điều này xảy ra, nó chỉ đơn giản tạo ra một nút lá cho cây quyết định và cho biết chọn lớp đó.

– Không có tính năng nào cung cấp bất kỳ information gain. Trong trường hợp này, C4.5 tạo ra một node quyết định (decision node) bằng cách sử dụng giá trị kì vọng của lớp đó.

– Với các trường hợp khác, C4.5 lần nữa tạo ra một node quyết định bằng cách sử dụng giá trị kì vọng của lớp đó.

Thuật toán được giải mã như sau:

Bắt đầu:

ComputerClassFrequency(T);

Kiểm tra các trường hợp cơ bản rồi tạo ra node quyết định

if OneClass or FewCases

return a leaf;

Create a decision node N;

Gán N.test = Thuộc tính với information gain được chuẩn hóa cao nhất

ForEach Attribute A

ComputeGain(A);

N.test=AttributeWithBestGain;

Thuật toán C4.5 sau đó sẽ lặp lại với các danh sách con nhỏ hơn và gán những node như là các node con

if (N.test is continuous)

find Threshold;

ForEach T’ in the splitting of T

If ( T’ is Empty )

Child of N is a leaf

else

Child of N=FormTree(T’);

ComputeErrors of N;

return N

Ví dụ mô tả cách tính information gain:

Với thuộc tính rời rạc:

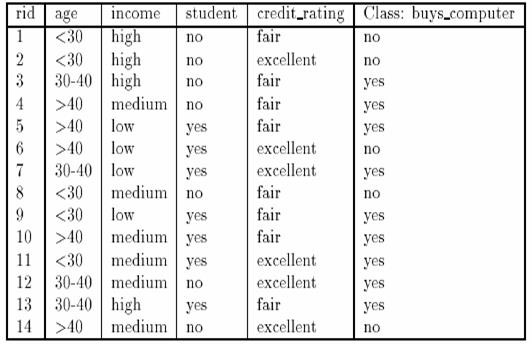
Trong tập dữ liệu trên: S1 là tập những bản ghi có giá trị phân lớp là yes, S2 là tập những bản ghi có giá trị phân lớp là no. Khi đó:

Tính G(S,A) với A lần lượt là từng thuộc tính:

A = age. Thuộc tính age đã được rời rạc hóa thành các giá trị <30, 30-40, và >40.

với age = “<30”:

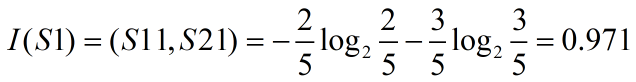
với age = “30-40”:

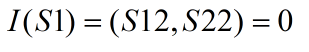
với age = “>40”:

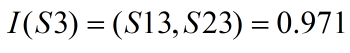
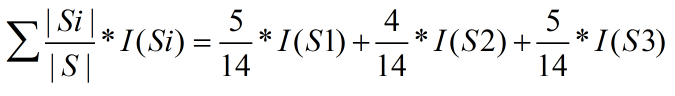
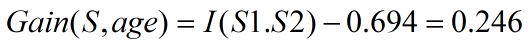
Tính tương tự với các thuộc tính khác ta được:
– A = income: Gain (S, income) = 0.029
– A = student: Gain (S, student) = 0.151
– A = credit_rating: Gain ( S, credit_rating) = 0.048
Thuộc tính age là thuộc tính có độ đo Information Gain lớn nhất. Do vậy age được chọn làm thuộc tính phát triển tại node đang xét.

III. KẾT LUẬN

Hiệu của phân lớp của cây quyết định (Series of Rules) phụ thuộc rất lớn vào training data. Chẳng hạn cây quyết định được tạo ra bởi chỉ giới hạn 10 samples training data trong ví dụ trên thì hiệu quả ứng dụng cây quyết định để dự đoán các trường hợp khác là không cao (thường training data phải đủ lớn và tin cậy)Cây quyết định là một phương pháp phân lớp rất hiệu quả và dễ hiểu. Tuy nhiên có một số chú ý khi sử dụng cây quyết định trong xây dựng các mô hình phân lớp như sau:
Có rất nhiều thuật toán phân lớp như ID3, J48, C4.5, CART (Classification and Regression Tree),… Việc chọn thuật toán nào để có hiệu quả phân lớp cao tùy thuộc vào rất nhiều yếu tố, trong đó cấu trúc dữ liệu ảnh hưởng rất lớn đến kết quả của các thuật toán. Chẳng hạn như thuật toán ID3 và CART cho hiệu quả phân lớp rất cao đối với các trường dữ liệu số (quantitative value) trong khi đó các thuật toán như J48, C4.5 có hiệu quả hơn đối với các dữ liệu Qualititive value (ordinal, Binary, nominal).

Sưu tầm
Trần Thụy Ngọc Hằng

Học Online

Học Offline

Machine learning decision tree (cây quyết định)